一.概述
　　根据道路上交通性质的不同，道路照明可分为机动车道路﹑交会区和非机动车道路三类[1]，它们的照明要求各不相同，机动车道路以亮度为主，辅之照度，而交会区和非机动车道路就以照度为主，有时辅之于垂直照度。
　　显然，通过照明的方法在晚上使路面上得到均匀的光分布是道路照明的目的，均匀的亮度分布和/或均匀的照度分布可以避免光分布不均匀造成的一些视觉上的疏忽﹑反应迟钝以致造成失误或误判，成为避免发生事故和正常进行社交的重要保障；同时一个良好的环境也会提高驾驶员或行人的识别能力和安全度，提高他们的信心，获得足够的安全感。因此，在机动车行驶的路面上产生等亮度的光强分布和在交会区及非机动车道上产生等照度分布的光强分布是道路照明设计追求的目标，也是道路照明灯具设计者要完成的任务。
　　光强分布至关重要，它表达的是路灯发出的光束在空间的形态和分布。光线落在地面上产生照度或从路面上反射的光线产生的路面亮度都可以通过它的数据计算得到。为了容易计算和表达路面上的亮度或照度，采用一种表达光强分布的合适的方法对开发﹑评价和计算等工作都是极有意义的。本文主要介绍路灯空间光强分布的表述形式。
　　二.灯具光强分布的表述方法[2]
　　从光源或灯具向空间发出光线，按照传统的形态，大体有这样的分布：
　　●光源向整个空间发出光线，即具有4π的空间特征；
　　●大多数灯具向半个空间内发出光线，即具有2π的空间特征。
　　当然，也有的灯具如庭园里的柱头灯也有向整个空间发出光线的情况。
　　此外，近年来迅速发展的LED光源都只向半个空间内发出光线，具有2π的发光特征。这需要引起灯具设计和照明设计者的关注。
　　1.如何将灯具发出的光线走向用坐标表达出来
　　发光体在空间光线的定位用一个球形网就能解决，该网相当于地球上的经纬度线组成的网。假如将球形网的南北极轴线按空间坐标XYZ的Z轴南北方向设置的话，再将一个灯具/光源放在一个球形网的中心，让它的发光中心轴对准球形网的一个特征的方向，例如南极或北极，这样一来，所有光线穿网而出，就能把全部的空间光线按照网上的角度坐标给定位和准确表示了，见图1。

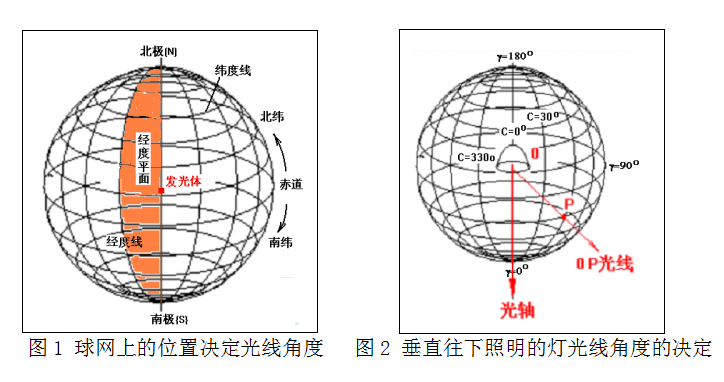
　　图2中，光线OP从球形网中心O点发出，穿出于网上P点，P点与网的关系可以用P点在网上的坐标表示。如像地球上各点的位置用经纬度的区分那样，将所有贯穿南北极的平面称经度平面，用C角表示，并认定一个起始平面称C=0°，如地球上的英国格林威治天文台的位置，那么所有光线所在的C平面都可以标定了。
　　在确定了光线在C平面上后，它的角度位置就可以像地球那样按照它的纬度确定下来。与地球上的纬度定义不同，地球某点的纬度从赤道(作0°)起始向南北两个方向算起:北纬XX度或南纬XX度，见图1。而光度学中规定从南极(作为γ=0°)往上算，一直算到北极(γ=180°)，见图2。
　　在光度学中，这种坐标系统就称C-γ系统，C相当于经度平面的角度，γ相当于该经度平面中的一个纬度角，某根光线的角度坐标就表达为(C，γ)。
　　实际应用时，球体的南北轴线还可以分别置于空间XYZ坐标中的另外两个方向X和Y上，得到另外两个标定发光体空间光线角度的形式，见图3。这就是光度学上的A-α系统和B-β系统。A和α及B和β分别是球体上的经度平面和纬度角的代名词。

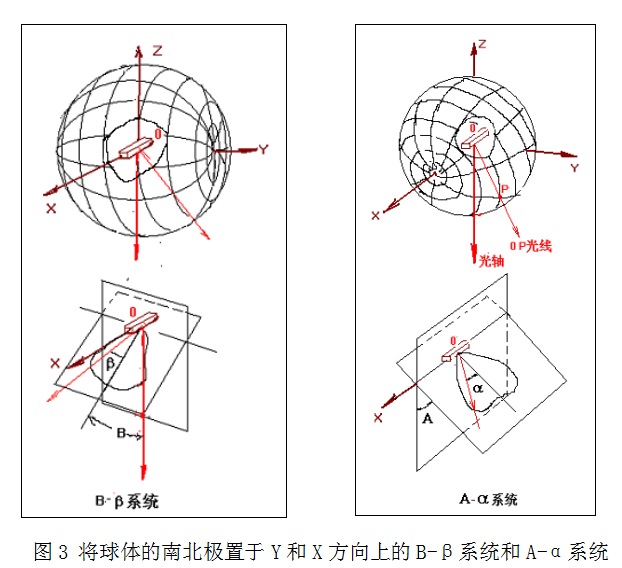
　　2.光线方向定标的规定过程
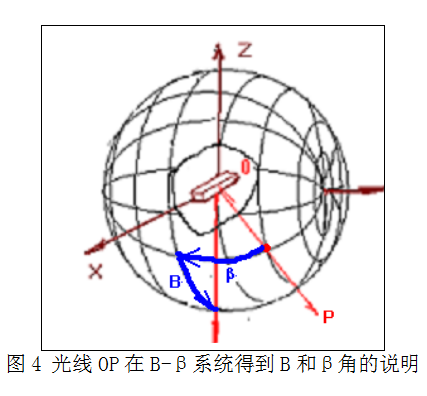
　　不管采用那个系统，光线OP的两个角度定义方法是相同的:先从该点P找到通过该点的经度平面，沿着该经度平面走到赤道，确定该点的“纬度角”α﹑β或90º-γ(说明:C-γ系统中的γ角采用的是补角，因此文中标出为90º-γ)，然后沿着赤道走到规定的起始的经度平面之间角度称A﹑B或C，最后得到该光线的角度坐标，A和α﹑B和β或C和γ的数值，图4是其中一个B-β系统中光线OP得到角度B和β过程的说明。

　　3.不同坐标系统之间角度的转换计算
　　同一根光线OP在不同坐标中的角度数值有A和α﹑B和β或C和γ，它们之间可以通过计算相互转换，计算比较繁杂，下仅列出它们间的关系式如下[2]:
　　由B-β坐标系统计算C-γ坐标:
　　cosγ=cosBcosβ，ctgC=ctgβsinB
　　由C-γ坐标系统计算B-β坐标:
　　sinβ=sinγsinC，tgB=cosCtgγ
　　由B-β坐标系统计算A-α坐标:
　　sinα=cosβsinB，ctgA=cosBctgβ
　　由A-α坐标系统计算B-β坐标:
　　sinβ=sinAcosα，ctgB=cosActgα
　　由C-γ坐标系统计算A-α坐标:
　　sinα=sinγcosC，tgA=sinCtgγ
　　由A-α坐标系统计算C-γ坐标:
　　cosγ=cosAcosα，tgC=sinActgα
　　4.空间坐标系统的选择
　　空间的一根光线可以用三个空间角度坐标系统来表述，因此就有三种光强分布表述同一个灯具的光空间分布，那么该如何使用这些系统呢?显然，选择中要遵循几个原则:
　　●选择的系统能清晰明了表示出灯具空间的光分布；
　　●该系统使灯具的光学设计和应用灯具时的照明计算变得简单明了；
　　●该系统能简捷明了地反映出一旦需要调节灯具(如安装高度﹑安装仰角)带来的变化。
　　根据上述原则，目前常使用的灯具选用的坐标系统是：
　　●室内灯(含工厂灯﹑筒灯等)：采用C-γ坐标系统，见图5。
　　●投光灯(含洗墙灯﹑舞台灯﹑射灯等)：采用B-β坐标系统，见图6。
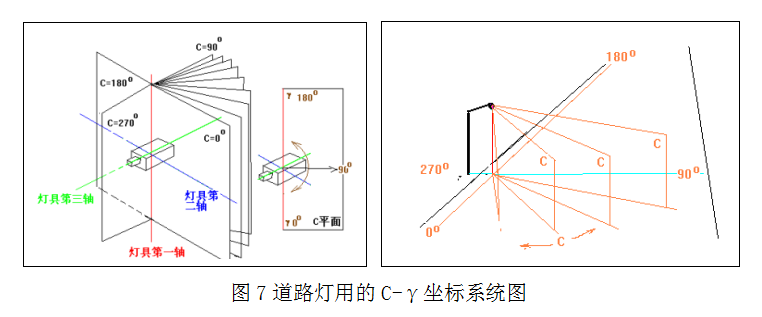
　　●道路灯(杆头灯和不调节仰角的路灯)：采用C-γ坐标系统，见图7。

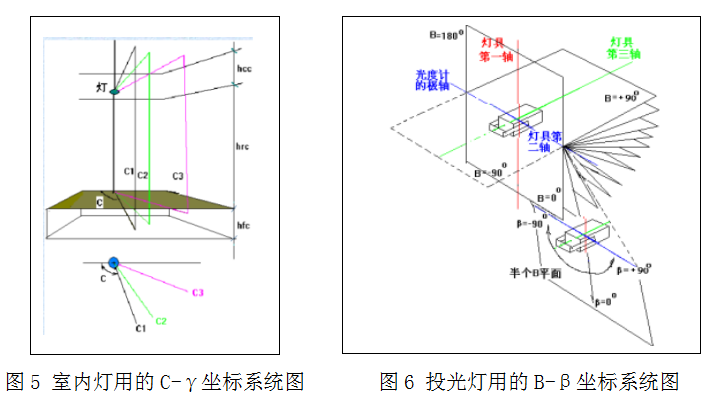
　　从各类灯具选用的角度坐标系统来看，使用和表述的方便是十分重要的。
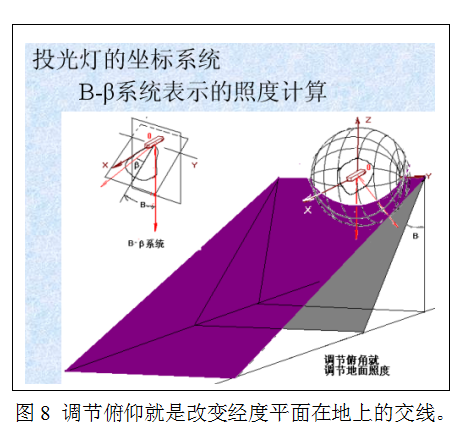
　　例如，对投光灯来说，调节俯仰角是使用过程中为了得到场地的均匀照明而必须采取的措施。采用B-β坐标系统的光强曲线后，球体上的经度平面与场地的交线就是一条条平行的直线，俯仰角的调节就变成改变球体上的经度平面与场地的交线。计算这些点上的照度变得十分简单明了，见图8。图上的两种颜色的平面就是两个经度平面，它们与场地的交线是直线。

　　三.路灯光分布的表述和应该选择的形式
　　从路灯在路面上安装的方法和位置来看，大部分路灯安装在路边的一侧向路面中心照射，因此，根据道路灯的配光和使用的情况有以下几个内容必须明确：
　　●空间的光强分布大多不具有旋转对称的特点(少数杆头庭园灯除外)，都只具有以垂直道路轴线平面为对称的平面对称特点，即按图7中以C=90°-270°平面为对称的光分布；
　　●对采用C-γ坐标系统的话，道路轴线在C=0°-180°平面内，从C=0°经C=90°到C=180°的范围内称路边，从C=180°经C=270°到C=360°(即C=0°)平面的范围内称屋边，主要研究的就是路边范围内的情况；
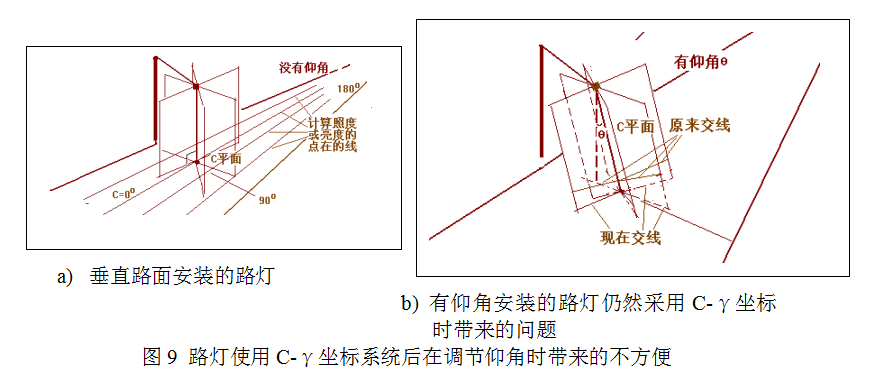
　　●在路灯的光轴垂直于路面时，使用C-γ坐标计算路面上各点的照度/亮度时，就像室内灯具计算被照面各点的数据一样。只要将路面上计算点的坐标在C-γ坐标的C平面内找到相应的γ角就可以了，见图9a。但一旦需要调节灯具安装仰角来获得更好的光分布时，此时路面上计算照度/亮度的点与原来垂直安装时的对应关系变得非常复杂，认识和计算都变得十分复杂甚至无法进行，见图9b。

　　为了简化调节仰角带来的问题，将C-γ坐标系统换成B-β坐标系统后，就可以将复杂的问题变得非常简单了。
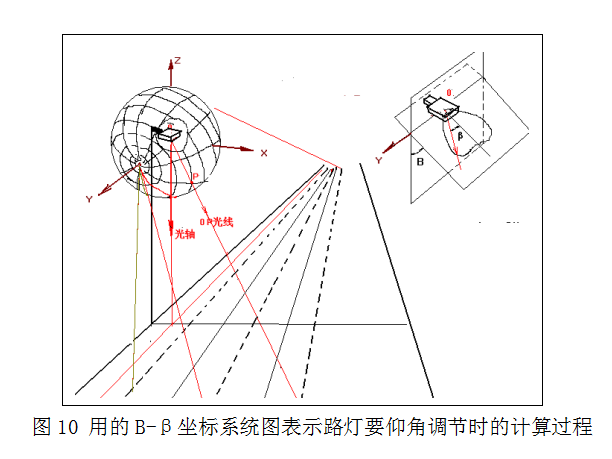
　　此时，道路上的每一条计算线都对应B-β坐标系统中的一个经度平面，查找射在该线上各点的光强变得非常方便，也不会出错。即使需要调节路灯的安装仰角，也仅仅只要再次改变B角，变动的角度就是仰角θ，所有被计算线上的点仍在一个个新的B角规定的经度平面上，换一个经度平面而已，例如从原来B1变成B1+θ而已。见图10。
　　从下一篇将谈到的道路上各条计算线的位置与路灯之间的对应关系就采用本文所述的B-β坐标系统的表述方法和内容，从而计算亮度需要均匀的路灯配光曲线的形状，因为路面上各条计算线都简单地对应一个B角代表的经度平面内的纬度角而已。

　　参考资料
　　[1]CJJ45-2006“城市道路照明设计标准”
　　[2]上海市照明灯具研究所编：灯具系统化设计1984。